04 Dec 2020

Convolution in CNN

这篇笔记是对 torch.nn.Conv2d [ 官方文档 ] 的解释，主要目标是弄清楚在这层 layer 中发生了什么：输入输出是什么？是怎么从输入到输出的？最后补充了一个困扰我很久的问题：为什么要叫 convolution?

Input/Output

文档中明确给出了输入输出的类型：有四个维度 (N, C, H, W) 的 tensor, 用 NumPy 的术语来说就是 4d array. 其中

N: Batch size, 即样本的个数，或者说一次计算操作的图片张数。注意，N 的大小完全不影响网络结构，所以它也没有出现在构造网络所需的参数表里。个人认为这个维度的存在完全是为了计算上的方便。因为对数据库中不同的图片进行的操作是完全一样的，所以在训练或者预测时不妨直接多张同时计算。显然，这个维度的大小始终不变。输入有多少张图片，输出就是多少张图片对应的计算结果。实际使用时让这个维度始终为 1 也可。当然，如果要进行 BatchNorm 操作，那输入样本数必须大于 1.
C: Channel size, 即图片的通道数。若输入是 RGB 图像，C_in 就是 3，若是灰度图像则为 1。注意，输出的 Channel size 是不一样的，C_out 应当理解为特征的通道。后面会提到，在计算每一个输出通道的结果时，所有输入通道的图像数据都被用到了。也就是说， 并不是 对 R G B 三个通道的图像分别进行同样的处理。这样即使输出只有 1 个通道，计算结果也会考虑颜色带来的影响。在构造 Conv2d layer 时的两个必要参数就是 C_in 和 C_out。实际使用时一般也仅需指定这两个参数 (外加一个 kernel size).
H & W: 图片高度和宽度。注意， height 代表的维度是在 width 之前的。所以像素坐标 (h, w) 代表的是图像从左上角开始数，向右数第 w 格，往下数 h 格的像素点。和数学中常见的第一个维度代表横轴，第二个维度代表纵轴非常不同。这两个维度的大小在输入输出中不必相同。 H_out, W_out 是依据 H_in, W_in 和一些其它参数自动确定的。这种依赖关系是 convolution 操作本身决定的，所以不能直接指定输出的大小，需要通过调整其他参数来间接实现。

总的来说，除去第一个维度 N, 输入和输出的 shape 是非常不同的. C_in, C_out 需要在设计网络时就确定好， H_out, W_out 则依赖于 H_in 和 W_out.

Parameters

在介绍 Conv2d 的各种参数之前，先简单地介绍输出是怎样从输入算得的。官方文档中给出的公式是 \[ output(N_i, C_{outj}) = bias(C_{outj}) + \sum_{k}^{C_{in}-1} weight(C_{outj},k) \star input(N_i, k) \] 其中 $\star$ 是 correlation 算符。

因为 input, output 都是 4d array, 所以指定 N, C 两个维度后得到的其实是矩阵。上式其实是矩阵等式。然后我们观察到 weight 和 N 无关，这在前面已经解释了，因为 N 这个维度相当于数据库中样本的编号，当然不可能每个样本都对应一套网络参数。但这不代表 weight 就少了一个维度，它仍然是 4d array, 只不过 shape 和输入输入稍有不同，是 C_out, C_in, K, K. 而 K 是 kernel size. 如果我们让 N 和 C_out 均为 1, 那么 output.shape 就是 1, 1, H_out, W_out, 等价于二维矩阵。此时的计算过程等价于用 C_in 个 K x K 大小的 kernel 分别对每个输入 channel 的图像矩阵作滤波然后 加权求和 。

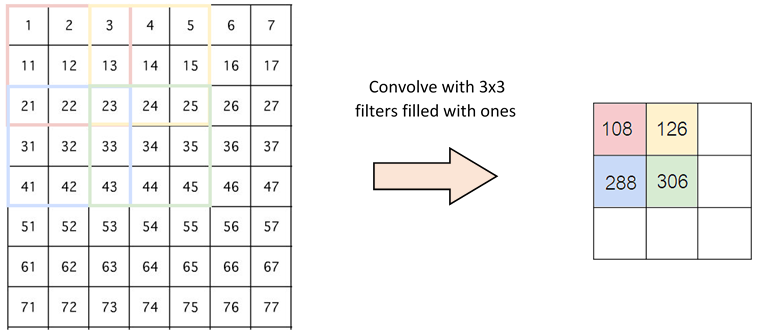
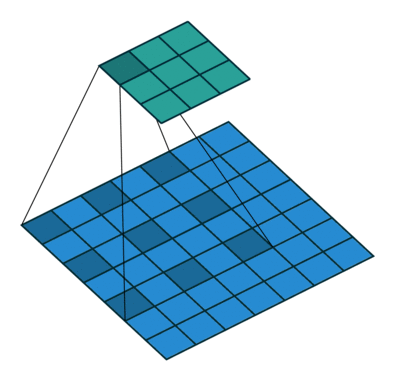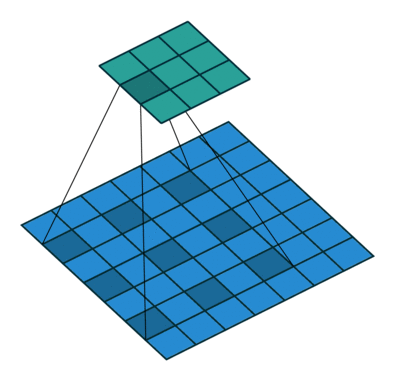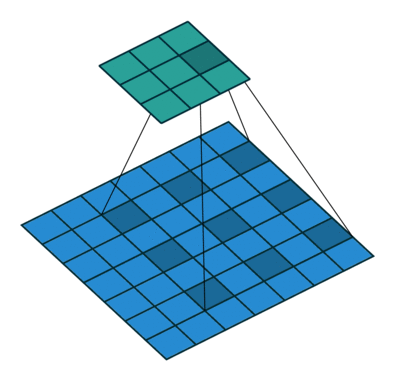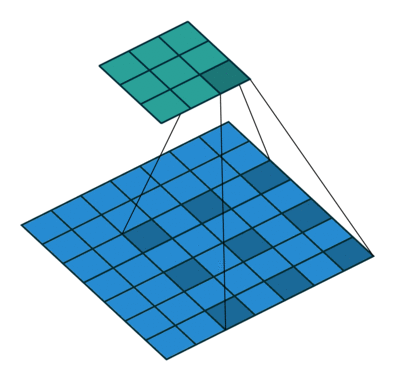
在最简单的情形， N, C_out, C_in 都是 1 时，只有一个 kernel，并且输入输出都可视为 2d array, 用 k 代表 kernel size. 那么输出可以写成

output[i,j] = dot(kernel, input[i:i+k, j:j+k])

这里 dot 表示将两个矩阵展开为一维向量后作内积。这个公式可以用下图形象地表述。

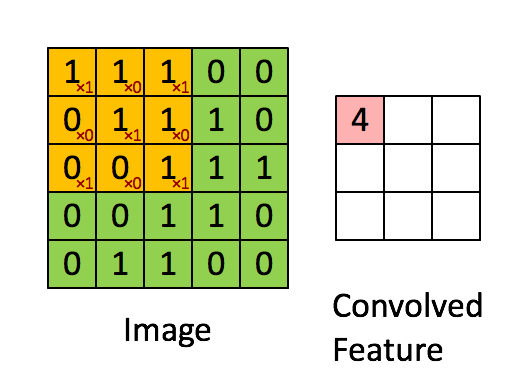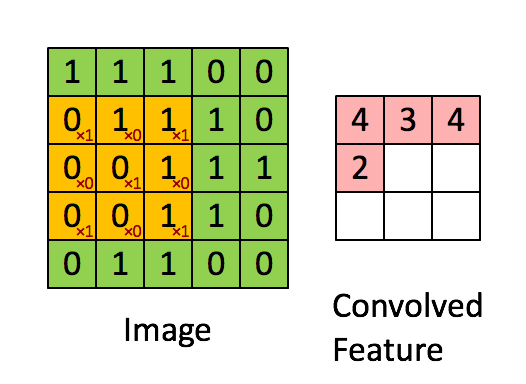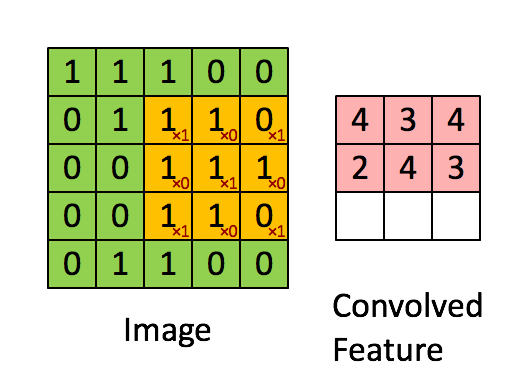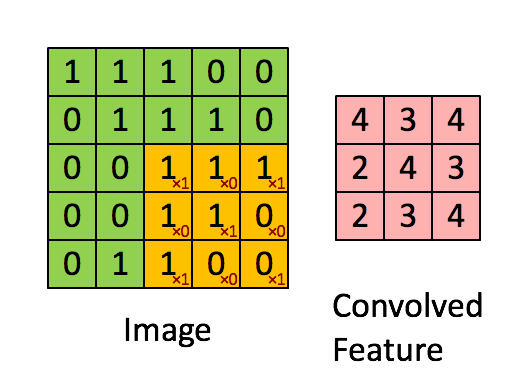
上图中绿色的 image 表示输入矩阵，黄色的 3 x 3 矩阵代表 kernel,右边的红色矩阵是输出结果。用这个公式可以计算出输出矩阵的形状。为了保证下标不越界，需要 i + k ≤ H_in, 同时 j + k ≤ W_out, 所以 \[ H_{out} = 1 + \max i = H_{in} - k + 1,\qquad W_{out} = 1 + \max j = W_{in} - k + 1. \]

stride

参数 stride 控制每次 kernel 滑动的步长，用公式表述就是

output[i,j] = dot(kernel, input[stride*i:stride*i + k,
                                stride*j:stride*j + k])

padding

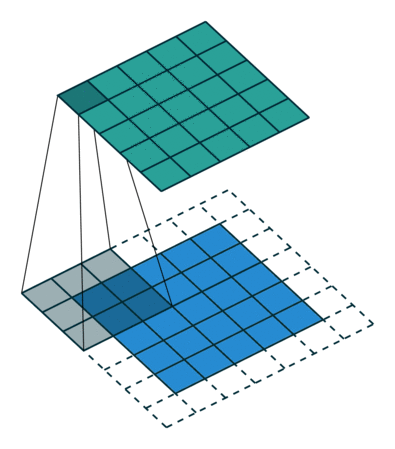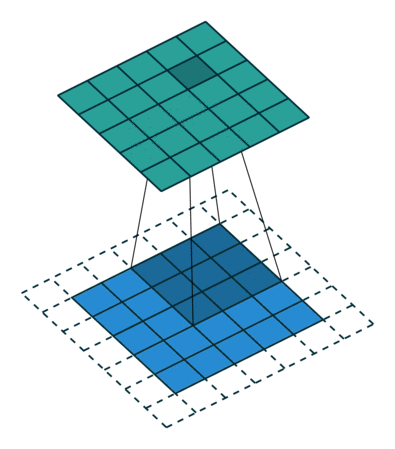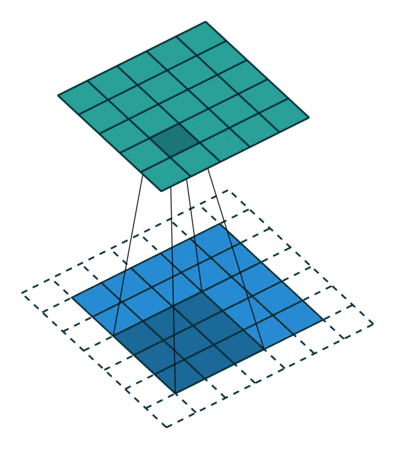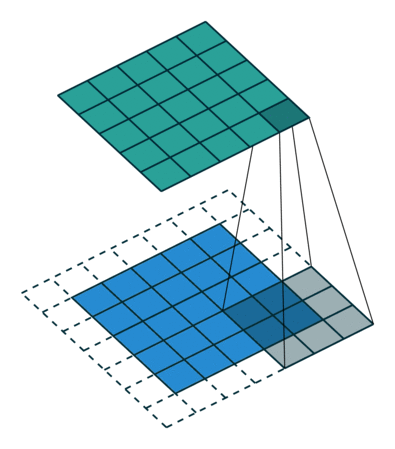
从之前的公式看出，一般输出矩阵的大小是小于输入矩阵的。要扩展输出矩阵大小也很简单，只要处理 input array 下标越界的问题就好了。之前的处理方式成为 valid padding, 即不允许下标越界。另一种处理方式是 zero padding, 即越界元素均视为 0. zero padding 也有好几种方式，根据对下标越界的容身程度而定。在 Conv2d 中用 padding 来控制 padding 方式。

padding=0 表示使用 valid padding, 不允许下标越界。
padding=1 表示使用 zero padding, 允许第一个指标为 -1 或 H_in，同时允许第二个指标为 -1 和 W_in 并令此类访问的结果为 0. 其他类型的越界不被允许。
padding=2 同理，允许在横向和纵向越界两个元素。

对于 3 x 3 大小的 kernel, 如果 stride=1, 那么只要设置 padding=1 就能让输出输出有相同的大小。

dilation

控制 kernel 如何覆盖在输入矩阵上，用公式表述就是

output[i,j] = dot(kernel, input[i:i+k*dilation:dilation,
                                j:j+k*dilation:dilation])

Correlation and Convolution

我最早接触的 correlation, convolution 是在光学课上，那里是对两个连续信号 f, g 定义的

$$ \begin{aligned} f \ast g (t) &:= \int_{-\infty}^{\infty} f(\tau) g(t-\tau) d\tau, \qquad ({\rm convolution})\\ f \star g(t) &:= \int_{-\infty}^{\infty} f(\tau) g(t+\tau) d\tau, \qquad ({\rm correlation}). \end{aligned} $$

所以数学上说，我们之前计算的并不是 convolution, 而是 correlation. 我个人认为 convolution 是沿用了之前 filter 的称呼，在那里 kernel 一般是中心对称的， correlation, convolution 计算结果相同。但最早没有接触图像处理中 filter 概念前这个称呼让我迷惑了很久，一直没想明白为啥明明做的是 correlation 却叫 convolution.